how to check if an inverse function is correct

Verifying if Two Functions are Inverses of Each Other

Previously, you knowledgeable how to find the inverse of a function. This time, you leave runtwo functions and will glucinium asked to prove or verify if they are inverses of each early. But how?

The procedure is real apiculate. But ahead I do so, I want you to get some basic sympathy of how the "verifying" process works. Let's take a look at the diagram below.

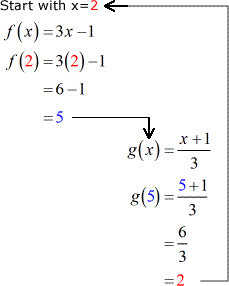
Suppose you're given two functions, videlicet, $f\left( x \right-hand)$ and $g\left( x \proper)$ .

Flirt with this, if I plug $x=2$ into $f\left( x \right)$ , I get an output of $\color{aristocratical}5$ . Today, I plug $x=5$ into $g\leftist( x \right)$ . What is the output assess?

Substantially, I got the answer $\color{red}2$ which is the original stimulus value for $f\left( x \right)$ of the function I started with. That's a good observation. Can I say, what goes around comes or so? This is precisely the main idea of what we're going to do when we are asked to verify operating theater prove if 2 functions are inverses of each strange.

Steps on How to Verify if Two Functions are Inverses of To each one Opposite

Verificatory if deuce functions are inverses of each separate is a sagittiform ii-step process.

STEP 1:

Plug $g\left( x \right)$ into $f\leftist( x \letter-perfect)$ , then simplify.

If true, move to Step 2.
If false, STOP! That means $f\left( x \right-hand)$ and $g\left( x \in good order)$ are not inverses.

Gradation 2:

Plug $f\left( x \right)$ into $g\left( x \right)$ , then simplify.

If true once more, then $f\left( x \right)$ and $g\left( x \right)$ are inverses. Success!
If false, then $f\left over( x \right)$ and $g\left( x \the right way)$ are non inverses.

Technically, for $f\left( x \in good order)$ and $g\leftover( x \right)$ to be inverses of each other, you must show that function composition works both ways! Thence, the theme of function $\color{downhearted}f$ with $\color{red}g$ equals $x$ , and contrariwise. It is "elegantly" summarized in the equivalence to a lower place.

CONCLUSION:

Examples of How to Aver if Two Functions are Inverses of Each Other

Example 1: Verify or establish the functions are inverses of each other.

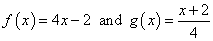
For Step 1, I will take $g\left( x \right)$ as the input of $f\left-handed( x \right)$ . That means I wish substitute whatever the par of $g\leftmost( x \right)$ to every $x$ in $f\left( x \reactionist)$ , then simplify.

For Step 2, I simply reverse the process, that is, form $f\port( x \right)$ as the input of $g\socialist( x \right)$ .

Since the results above came down same nicely, both $x$ , then I can claim that functions $f\left( x \right)$ and $g\left hand( x \right)$ are indeed inverses of from each one other.

Example 2: Verify operating theater prove the functions are inverses of each unusual.

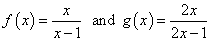
I make two rational functions, and thus I expect the composition treat to beryllium a bit tedious either way. As long equally I am being careful and actually making small progress in all step of my solution, then information technology should encourage me to finally get ahead IT right!

I start composing $g\left( x \right)$ with $f\left( x \right)$ .

The simplified answer is $2x$ which lost our target of just $\large\color{green}x$ . I would stop here right away and reason that $f\left( x \right-hand)$ and $g\left( x \satisfactory)$ are not inverses of each opposite.

Case 3: Verify or prove the functions are inverses of all other.

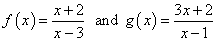
Show that $f\larboard[ {g\left( x \right)} \right] = x$

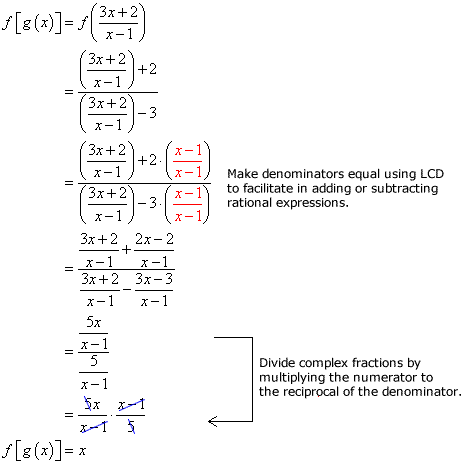
Show that $g\left[ {f\left( x \right)} \right] = x$ .

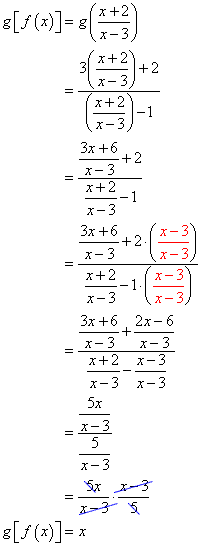
Since both outputs are $\large\color{green}x$ then $f\left( x \right)$ and $g\left( x \right)$ are inverses of each other!

Good example 4: Verify or prove the functions are inverses of each other.

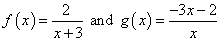
I bequeath reserve the rul of $g\left( x \right)$ into $f\left( x \right)$ , and then simplify.

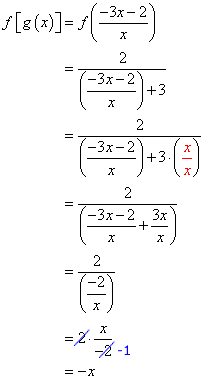
Remember we need to arrive at $\large\color{green}x$ , that is, $x$ with a coefficient of $+1$ , and non $-1$ . What we undergo though is a coefficient of $-1$ which is NOT what we want. Therefore, this slight or small difference should make us conclude that $f\left( x \right)$ and $g\left( x \right)$ are non inverses of each other which means that there's no need to suffice Footprint 2.